1. Find a 2-factorization of the following, or explain why no 2-factorization exists:
   1. K_4,4

      I will use {a, b, c, d}, {x, y, z, w} as the two parts of K_4,4. Since each point has degree 4 and each 2-factor of the factorization uses 2 edges, there must be two 2-factors in any 2-factorization of K_4,4.

      First remove the 2-factor (cycle) axbyczdwa now consider the graph that remains is the 2-factor (cycle) aydxcwbza. These two cycles form a 2-Factorization (in fact a Hamiltonian factorization) of K_4,4.

      Note that there is another answer in which each 2-factor of the 2-factorization consists of two 4 cycles.

   2. K₈

      This cannot have a 2-factorization as there arepoints of odd degree.

   3. K₉

      I will use {x, 0, 1, 2, 3, 4, 5, 6, 7} for the point set of K₉. A method for finding 2-factorizations was given in the notes. x is the 'infinite' point, so x + 1 = x and x + 2 = x, all other arithmetic is mod 8. Start with the 2-cycle x01726354, and add 1 (mod 8) and 2 (mod 8). Thus the full 2-factorization is:

      x01726354, x12037465, x23140576

2. 1. Find a decomposition of the bowtie into triples (C₃) abc, cad, bde, dce, efh, egf, fih, ghf.

      Note that this was done "by inspection".

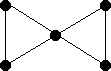
      The two triangles of the bowtie each form a C₃.

      Note that this question asks for a decomposition, not a factor or factorization. This essentially means that we only need to C₃'s which decompose the edge set and they need not be disjoint. This graph does not have a factorization into C₃'s as that would require sets of disjoint C₃'s which cover the point set. Indeed this graph does not even have a 2-factor.

   2. Find a decomposition of the graph below into cycles. Explain why no C₃ decomposition can exist.

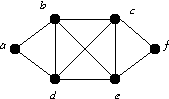
      Decomposition into a C₆ and a C₄:
      C₆: abcfeda, C₄: bdceb

      Alternately, decomposition into a C₄ and two C₃:
      C₄: dcdeb, C₃: abda, C₃: fcef.

      If we try to decompose into C₃s, the points a and f must appear in the triples abda and fcef respectively. The remaining edges form a 4 cycle, and contain no more C₃s.

   3. Find a decomposition of Q₃ into a 1-factor and a 2-factor.

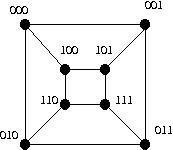
      First remove the 1-factor {000, 100}, {001, 101}, {111, 011}, {110, 010}. The remaining edges are now a 2-factor (two disjoint C₄s).

   4. Find a factorization of the K₁₅ into triples (C₃)

      This is the original Kirkman's Schoolgirl Problem:

      Fifteen young ladies in a school walk out three abreast for seven days in succession:
      it is required to arrange them daily so that no two shall walk twice abreast.

      Labeling the schoolgirls a - o the following is a solution:

      Monday	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
      abc djn ehm fio gkl	ahi beg cmn dko fjl	ajk bmo cef dhl gin	ade bln cij fkm gho	afg bhj clo dim ekn	alm bik cdg ejo fhn	ano bdf chk eil gjm

      Note that there are 80 non-isomorphic solutions. And of course relabeling will produce a different looking solutions.

3. Find the chromatic number χ(G) and the chromatic index χ'(G) for each of the graphs below. In each case give the colour classes of a minimal colouring.

   1. 

      χ(G) = 3. χ'(G) = 4.

      Note that this graph contains a K₃, so χ(G) is at least 3. It is not hard to find a 3 colouring of the vertices.

      Since the graph contains a vertex of degree 4, χ'(G) is at least 4. It is not hard to find a 4 colouring of the edges.

   2. 

      χ(G) = 3. χ'(G) = 4.

      Note that this graph contains a K₄, so χ(G) is at least 4. Here are the colour classes of a 4-colouring":

      C₁ = {b, f},
      C₂ = {a, c},
      C₃ = {e},
      C₄ = {d}.
      

      Δ = 4, so χ' is at least 4. Here are the colour classes of a 4-edge colouring":

      C₁ = { bc, ad, cf },
      C₂ = { be, cd },
      C₃ = { bd, ce},
      C₄ = { ab, cf, de }.
      

   3. 

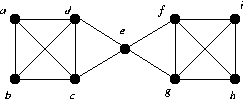
      Note that this graph contains a K₄, so χ(G) is at least 4. In fact χ(G) = 4, here is a 4-colouring C_i is the coulour class i.

      C₁ = {e, a, i},
      C₂ = {b, f},
      C₃ = {c, g},
      C₄ = {d, h},
      

      Note that the maximum degree Δ = 4, so χ'(G) is either 4 or 5 by Vizing's Theorem. In fact χ'(G) = 4, here is a 4-colouring C_i is the coulour class i.

      C₁ = { ef, gh, dc, ab},
      C₂ = { eg, fi, ac, bd},
      C₃ = { ec, ad, fg, ih},
      C₄ = { ed, bc, fh, gi},
      

   4. 

      This graph is bipartite, so χ'(G) = 2:
      C₁ = {000, 011, 101, 110},
      C₂ = {001, 010, 100, 111},
      

      Note that this is exactly the partition of Lab 1 Question 1.

      Since Q₃ is 3-regular, Δ = 3, and so χ'(G) is either 3 or 4 by Vizing's Theorem. In fact it has a 1-factorization, this is a 3-colouring of the edges.

      C₁ = { {000 001}, {100, 101}, {110, 111}, 010, 011} }
      C₂ = { {000, 010}, {100, 110}, {101, 111}, {001, 011} },
      C₃ = { {000, 100}, { 001, 101}, {010, 110}, {111, 011} }.

4. Given a minimum colouring of a graph G, show that for each colour class C_i there is some vertex v ∈ C_i which is adjacent to a vertex of each of the other colours.

   Suppose not, that is suppose that there is a minimum colouring such that every vertex in the class C_i is not adjacent to a vertex of some other colour.
   But if a vertex u in C_i is not adjacent to a vertex of some colour j, then u can be re-coloured j.
   Proceeding in this way for every vertex in C_i will empty C_i and produce a smaller colouring.
   This contradicts the assumption that the colouring was minimum already.

5. Let G be a k-regular bipartite graph, show that G has an r-factorization if and only if r divides k.
   (You may assume that every k-regular bipartite graph has a 1-factorization.)

   (⇒) Necessity was done in the lectures.

   (⇐) Let G be a k-regular bipartite graph, and r, s are an integers such that k = rs.
   Since G is k-regular bipartite it has a matching M₁ (Corollary of Hall's Theorem).
   Now since each vertex of G appears with degree 1 in M₁, G - M₁ is a k-1 regular graph.
   Further deletion of edges cannot violate the bipartite property, so G - M₁ is bipartite.
   So G - M₁ is a k-1 regular bipartite graph and so has a matching M₂.
   We proceed in this manner until we have r matchings M₁, . . ., M_r.
   Now F₁ = M₁ ∪ . . . ∪ M_r is an r-factor of G.
   We have shown that any k regular bipartite graph G with k ≥ r has an r-factor.
   Removing the edges of this r-factor results in a new graph G₁ which is k-r regular bipartite and so has a r-factor.
   Continue removing s r-factors as above, k - sr = 0.

Peter Danziger, April 2008