Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 1 Solutions

We will work on these questions in the lab.

  1. Consider the graph Qn whose vertices are labeled by strings of length n over {0, 1} (binary strings of length n, eg when n = 3, 000, 001, 010 etc.) There is an edge between to vertices if the strings that label them differ in exactly one place. In general Qn is known as the n-cube.

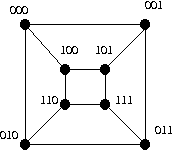
    So, for example there is an edge between 000 and 010 which only differ in the second position, but not between 000 and 110 which differ in two places nor between 000 and 111.

    1. Draw Q3.
    2. Is Q3 bipartite? If so give a bipartition.

      Yes. Take
      V1 = {000, 011, 101, 110}
      V2 = {111, 001, 010, 100}

    3. In general, for what values of n is Xn bipartite?

      In general vertices labeled with bit strings containing an odd number of 0's will never have an edge between them (since they must differ in at least 2 places). Similarly strings with an even number of zeros will never be adjacent. This provides a partition of the vertices, so yes for every n > 1.

      Note that the above in fact assumes that n > 1.

  2. Generalizing from the previous question define the graph Q(n, t) to be one whose vertices are labeled by strings of length n over {0, 1} (binary strings of length n, eg when n = 3, 000, 001, 010 etc.) There is an edge between to vertices if the strings that label them differ in exactly t places.

    [Note misprints fixed: q(n, 0) -> Q(n, n) in each case]

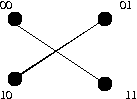
    1. Draw Q(2, 2) and give its adjacency matrix.
      0 0 0 1
      0 0 1 0
      0 1 0 0
      1 0 0 0
    2. Draw Q(3, 3).
    3. Give a characterization of Q(n, n) for any n. Justify your characterization.

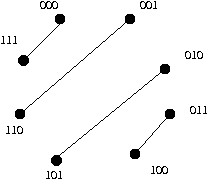
      For any n Q(n, n) will be a "perfect matching", that is each vertex will be paired with exactly one other vertex. A given vertex will be adjacent to the vertex who's bit-string label is exactly the complement (opposite) of the given one - 1's and 0's exchanged.

  3. Not Given

  4. For each of the following graphs indicate whether the are subgraphs of K3,3 or the complement of K3,3. In each case justify your answer.
    1. P5.

      Yes. (Trace it out)

    2. C5.

      No. K3,3 is bipartite and no bipartite graph can contain an odd cycle.

    3. K5.

      No. Each vertex in K5 has degree 4, whereas all vertices in K3,3 have degree less than 4. OR K5 has 10 edges whereas K3,3 only has 9.

    4. K2,3.

      Yes. K2,3 is induced from K3,3 by deleting any vertex.

  5. Show that at any party with at least 6 people there are either 3 mutual strangers or 3 mutual acquaintances.

    Proof: Consider the acquaintance graph G. We will prove that either G contains a triangle (K3) or 3 independent vertices by considering the possible degrees of the vertices of G. [Note that it helps to draw the relevant pictures.]

    We will attempt to create a graph of order six, which contains no triangle.

    Suppose that there was a vertex v with degree 3. Then there can be no edge between the neighbors of v since this would create a triangle. On the other hand the neighbors of v are now an independent set of size 3. Thus any vertex can have degree at most 2. Note that this means that the maximum number of edges is 6.

    If every edge has degree 2 we have that G is a union of disjoint cycles. Either G is two triangles, which contains a triangle, or G = C6, which contains 3 independent vertices. So G has less than 6 edges.

    If G contains a vertex v with degree 0, there must be two other vertices u and w say, which do not form an edge (since there are at most 5 edges for the 5 remaining vertices). But now u, v, w would be an independent set of size 3. So there are no vertices of degree 0.

    If G contains a vertex v with degree 1, there must be another vertex u also of degree 1 (the number of odd degree vertices is even). If uv is not an edge there is are two vertices wich are neighbors of u and v leaving least 2 vertices which are adjacent to neither u nor v. One of these together with u and v form an independent set of size 3. If uv is an edge either the remaining edges all have degree 1, which yields 3 independent vertices, or they form a C4, which also gives 3 independent vertices.

Maintained by: P. Danziger, January 2007