Garnet Ord
Ryerson University/PI
Abstract
Bohmian trajectories and Feynman paths are conceptually different objects from radically different views of quantum mechanics. Both offer different `particle pictures' in a subject that is based on wave mechanics. Some recent models of subquantum dynamical processes underlying the Dirac equation suggest that there may be an unexplored link between the two concepts via the quantum potential. We sketch the qualitative ideas involved and view some simple implementations that quantitatively illustrate the suggested link.
October 2005
The domain of this talk is propagation in elementary, single particle quantum mechanics. The tools are simple but non-standard for discussions of quantum mechanics. We shall use only classical statistical mechanics. The target of the talk are solutions of equations like:
 | (1) |
Where H is a simple Hamiltonian. From a quantum mechanical perspective, ψ is important as an element of a probability calculus. However there is no agreement within the physics community as to whether ψ represents anything in an external physical reality.
In classical statistical mechanics the task is simply to count recognizable objects. If we can arrive at Eqn. (1) using only statistical mechanical tools, we will have a context in which ψ itself is recognizable in its own right.
Roughly speaking, there are two categories of ‘pictures’ in the interpretation of quantum mechanics, based on whether there is an external reality that contains objects resembling classical particles.
![[Graphics:HTMLFiles/index_7.gif]](HTMLFiles/index_7.gif)
Figure 1. Figure from “The Road to Reality” by Penrose[1].
If we ignore the fact that individual electrons are detected, the diffraction pattern of the double slit experiment has a natural interpretation in terms of waves. When we notice that the pattern is formed by individual particle-like events, we either need a collapse phenomenon at the detector, or we need to strengthen the particle paradigm.
How do you obtain nodes in a particle-based theory? Bohms theory uses solutions of the wave equation to construct a quantum potential. The potential establishes path-rich and path-poor areas in a wave pattern.
![[Graphics:HTMLFiles/index_9.gif]](HTMLFiles/index_9.gif)
Figure 2. From “ The quantum theory of motion” by Holland[2].
What about Feynman paths? These are not considered real, as Bohm paths are, however it is interesting to see how wave patterns are built. In particular, in terms of Feynman paths, nodal regions are not path-poor, they are path-paired where the opposite phase of pair members cancel.
![[Graphics:HTMLFiles/index_11.gif]](HTMLFiles/index_11.gif)
Figure 3. In the double slit experiment, nodes are created by a pairing of oppositely phased paths through the two slits.
(Compare Feynman phase factor 
with the Wiener integral Boltzman factor 
. The Boltzman factor is the result of just counting trajectories, the Feynman phase appears to be counting wave amplitudes.)
(eg. If we wanted the lighting lowered in this room we would request that the lights be dimmed, we would not expect that a‘darkness projector’ be turned up to reduce the ambient light. )
Suppose we assume paths (world-lines) that are continuous, begin before t =0 and end beyond the time scale of interest. These simple paths, where x is a single-valued function of t, are counted with the natural numbers Ν. The diffusion equation may be shown to be a continuum limit of a counting process for a particular kind of such paths.
![[Graphics:HTMLFiles/index_16.gif]](HTMLFiles/index_16.gif)
FIG. 4: Two simple paths. Only positive integers required to count the number of paths.
Suppose however that paths are continuous and traverse a particular time interval of interest, but this time they can double back! Now 
is not a single-valued function of t anymore. If we want to count such paths, we have to count taking into account the direction of traversal! In the figure below, the path is colour coded to indicate direction of traversal, blue for forward in t, red for backwards in t. If we associate a +1 with blue and a -1 with red, the sum of all contributions at fixed t will count the number of paths. Note we now need the integers Z to do our counting.
![[Graphics:HTMLFiles/index_19.gif]](HTMLFiles/index_19.gif)
FIG. 5: Continuous paths with reversed segments require the negative integers for counting paths. At fixed t the number of continuous paths is the number of blue contributions minus the number of red.
Can we construct a single non-simple path in such a way that it mimics solutions of the Dirac equation? If we can, we have a chance to understand quantum propagation in a way that is similar to Einstein’s explanation of diffusion in terms of Brownian motion.
The Dirac Equation is usually produced by arguments that begin by requiring a PDE of the 
form ( h
)
 | (2) |
This is followed by the relativistic requirement that
 | (3) |
where 
is the rest mass of the electron and 
is the momentum. Combining these requirements lead Dirac to propose
 | (4) |
Iterating Equation 2 , using Equation 3 suggested the usual anticommutation relations for the matrices 
and 
. Much as the original argument was brilliant and insightful, there was no sense in which the resulting equation described a wavefunction 
that had a 
.
Here we imagine deriving the Dirac equation in 1+1 dimension for an accountant who is of course familiar with simple arithmetic, notably counting with integers and using rational numbers when a reason for division of integers is explained.
Equation 1 would have little meaning for our accountant. i =
is outside common arithmetic as are Real numbers and the calculus. However, counting configurations of a stochastic process on a lattice is within the domain of accountancy tools. Consider the stochastic walk considered in Fig. 6
![[Graphics:HTMLFiles/index_34.gif]](HTMLFiles/index_34.gif)
FIG. 6: On the left is a single `entwined path' in the 
plane. The colour indicates the direction of traversal, blue for traversal in the 
direction, red for traversal in the 
direction. The origin is at the bottom of the path and the lattice spacing is small on the scale of the figure. Notice that the crossing of the forward(blue) and backward(red) paths forms a chain of oriented areas. The orientation switches from one rectangular area to the next. This is illustrated by the recolouring of the path in the centre figure. There blue represents positive orientation and red represents negative orientation. To count oriented rectangles we can simply use the `enumerative' path, illustrated on the right hand side of the figure. Here the colouring illustrates the contribution to orientation, +1 for blue, -1 for red.
We consider a special ``entwined'' walk on a square lattice in the (x,y)-plane[3-5]. The lattice spacing will be some small positive rational number ϵ and the walker will move at each step in one of the four directions 
. The stochastic element of the walk is governed by the binomial distribution. That is, at step n+1, the walker will step in the same direction as in step n with probability
, with m a fixed positive constant and
. The alternative at each step, besides continuing in the same direction, is a change of state. A change of state occurs in an alternating pattern. The walk is started from the origin and the first step is to (1,1). The stochastic process is consulted and the walk continues to 
unless a state change is indicated. The first state change is a change in the direction of motion along the 
-axis. So if this happens at 
, the subsequent step is to 
. The next state change will not change the direction of the walk, but the walker will drop a marker for its return path before stepping to the next site. Thus all the odd numbered state changes will be direction changes in the x coordinate, all the even numbered state changes will preserve direction but drop markers. This process will continue until the walk steps past some pre-assigned y-coordinate, 
say, at which point, at the next marker drop, the walker will return to the origin along the path defined by the set of markers. A single such entwined path(EP) is illustrated in Fig1.
Notice that the EP defines a chain of oriented rectangles in which the orientation reverses at each crossing point of the EP. If we use the `right hand rule' for path traversal, the first rectangle has positive orientation out of the page, the second negative, into the page, and so on in an alternating fashion. As the walk is lengthened by repeating the process we can imagine that a cone with apex at the origin will become covered by an ensemble of these oriented rectangles. If we sit at a particular off-lattice point inside this cone we could expect to be regularly encircled by these oriented rectangles and we might expect that we should eventually see an equilibrium distribution of orientation, varying from point to point throughout the cone. How could we measure this orientation?
Consider again Fig1. Each oriented rectangle has a left and right boundary that contributes to the oriented area. So as to avoid counting the contributions of an area twice let us restrict our attention to the right boundary of each rectangle. The collection of right boundaries itself forms a path that we call the 'enumerative path' . Note that the enumerative path has a very regular structure and we can use it to count oriented rectangles. The blue segments of the path belong to positively oriented rectangles and add a +1 to the oriented area count. The red portions of the enumerative path belong to negatively oriented rectangles and contribute a weight of -1 to the count.
Now our task to count oriented rectangles is reduced to counting the contributions of enumerative paths on the lattice. We can do this using the structure of the walks to deduce what the equilibrium pattern, assuming there is one, must be.
Let us label the lattice sites by 
, and 
where 
and 
are integers. We consider a two component density 
where 
counts the number of 
and 
directed links and 
counts the number of 
and 
directed links 
. We need a 2-component density here because our enumerative paths continually shuffle orientation counts between the two directions.
Now any link at 
in the 
direction either follows a link of the same direction and colour at 
or follows a link of the opposite direction and colour at 
. The former occurs with probability 
, the latter with probability 
. Thus if an equilibrium density is reached it must satisfy:
 | (5) |
Notice here the subtraction involved in the second term. This is because whenever our enumerative path `turns right' it switches orientation, thus changing the sign of its contribution. Since this happens for all paths, it must happen for the equilibrium distribution. We can similarly deduce that the 
density must obey the difference equation:
 | (6) |
The positive sign for the second term reflects the fact that the change of direction for a `left turn' on an enumerative path does 
change orientation.
Equations 5 and 6 are difference equations that, with suitable initial conditions for the 
yield rational number solutions inside the cone above the 
-axis. The equations themselves are just conservation equations that express the fact that the enumerative paths are continuous and have the alternating orientation of Fig1. The solutions 
spread out into ever larger regions along the 
-axis as 
increases, so 
includes an exponential decay. We may choose to look through this background decay to see the emerging pattern by following the evolution of:
Write
 | (7) |
then 
satisfies the equations:
 | (8) |
to lowest order in 
.
Let us now pause and note that Eqn(\ref{diffs}) is a perfectly respectable equation for an accountant to produce. There are no abstractions or mathematical tools involved that take us out of the domain of good accountancy. We know exactly what is being counted \ldots oriented rectangles produced by a long entwined path. We know the number system involved ... the counting actually just used integers but the use of probability and normalization placed us in the domain of rational numbers. We {\em have} assumed that an equilibrium pattern will emerge from our initial conditions but that is something that is easily checked by performing a numerical experiment. Indeed, the calculation up to this point involves only a basic counting of recognizable objects on a planar lattice.
We abandon the limitations of arithmetic and approximate the solutions of (8) by taking a continuum limit. If we subtract 
from both sides of (7), divide by 
and take the limit as 
we find that
or writing
we have
 | (9) |
This may be recognized as a form of the Dirac equation where 
and 
. Note that if we iterate this equation to get a second order form we have
 | (10) |
which is the Klein-Gordon equation.
Note, this means that the solutions of these ‘wave equations’ are a continuum limit of a pattern formed by the a counting process for a single ‘space-time’ trajectory!
Notice that to obtain the Dirac and Klein-Gordon equations above we have not invoked :
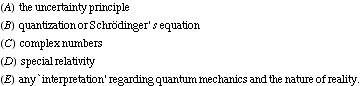
We have simply taken the output of an `accounting argument' and written it in a language familiar in the context of relativistic quantum mechanics.
Now (9) 
just a continuum limit of (8) written in a familiar form. (Notice that there has been no analytic continuation forced on the system. 
is real and the 
in (8) is present only because 
is imaginary.) The point here is that we can regard (8) either as a fundamental equation about the 'wavefunction' of an electron, without knowing exactly what a wavefunction represents in the physical world, 
we can take (8) as the continuum limit of an equation describing an equilibrium distribution of a simple stochastic process. The continuum language that we use does not tell us whether we are describing a `Dirac wavefunction in one dimension' or a `spacetime that maintains an accountancy ledger for the EP stochastic process'.
In the context of quantum mechanics, all ‘ derivations’ of quantum mechanics from particle mechanics involve a formal analytic continuation (FAC), either explicit or forced by a global requirement. For example:
is an explicit FAC that takes us from real dynamical variables to complex operators.The above derivation of the Dirac equation has no such analytic continuation, either explicit or globally forced. So what makes it work???
Historically and to a certain extent logically, the evolution of number systems is something like:
N -> Z ->Q -> R -> C
N, Z, and Q are appropriate number systems for the counting problems of classical statistical mechanics. However in making the transition from classical mechanics to quantum mechanics, we habitually start in R (we need a smooth continuum for classical mechanics) and we are forced into C by ‘wave-particle duality'.
In the ‘Accountant version’ we started with a counting problem for non-simple curves. This forced us to use Integers for the primary number system. The geometry (counting oriented areas) required that the counting have a 2-component structure with a built-in periodicity. The continuum limit of the counting process then contained the algebra of the complex numbers, not just the Reals. The logical structure is something like:
where 
and 
are essentially subsets of 
with discrete phase and modulus. The difference here from other derivations of the Dirac equation is that the Algebra of complex numbers is built by a combination of the local geometry of the trajectory and the counting process that detects oriented areas. The natural extension of the counting process is to 
, not 
. Unfortunately the connection between the ‘subquantum dynamical process’ and the resulting ‘wavefunction’ is lost in the continuum limit because the process itself is below the resolution of the resulting partial differential equation. ( compare thermodynamics and stat. mech.)
... See Animation
Q. How robust is this? Does the Dirac equation depend on minute details in the geometry and/or the stochastic process?
A. Apparently not. The geometry has to be periodic, and there has to be a strict pairing of forward and return paths. The dynamical process can be stochastic, but it is vastly more efficient to have the dynamics deterministic and input the stochastic element at the initial conditions.
Q. The argument was for 1+1 dimensions. What about 3+1.
A. This seems to be a fairly straight-forward extension ... but it has not received a critical appraisal by anyone else yet.
Q.What is the analog of superposition in this context?
A. Concatenation. Any two space-time patterns A and B formed by entwined paths from the same origin form the pattern A+B when the trajectories are concatenated.
Q. It is known that the real difficulty with quantum mechanics is ‘measurement’. The toy model only covers propagation. Why would this be an advantage given we already understand propagation in terms of waves.
A. The problem with waves is that you are hard pressed to figure out why measurement favours particles. If, as in the toy model, the underlying dynamical process produces a particle-like trajectory, the hope is that the measurement problem will be lessened.
Q. What about relevance to the Bohm picture.
A. At this point they could be connected in a rather artificial way. A (deterministic) entwined path can ‘write’ the appropriate wavefunction on a region of spacetime given the correct initial condition. To mimic Bohm we could instruct the particle to so write the appropriate wavefunction and at then finally exit the spacetime region via the Bohm path determined by the previously written wavefunction.
Q. What about multi-particle quantum mechanics?
A. Still to be looked at.
![[Graphics:HTMLFiles/index_110.gif]](HTMLFiles/index_110.gif)
Figure 7. The first excited state of a particle in on a ring. This is the ‘wavefunction’ propagated by a single entwined path that traverses the spacetime region given the appropriate initial condition at t=0.
This assumed:
| [1] | Penrose, R. (2004). <BookTitle>. <City>: Jonathan Cape. |
| [2] | Holland, P. R. (1993). <BookTitle>. <City>: Cambridge University Press. |
| [3] | Ord, G. N., & Mann, R. B. (2003). Entwined pairs and Schrødinger's equation. Annals of Physics, 308(2), 478-492. |
| [4] | Ord, G. N., & Gualtieri, J. A. (2002). The Feynman Propagator from a Single Path. Phys. Rev. Lett, 89(25), 250403-250407. |
| [5] | Ord, G. N., & Mann, R. B. (2003). Entwined paths, difference equations and the Dirac equation. Phys. Rev. A, 67. |