1. For each of the graphs below: In Each case state whether the given graph is
   1. State whether it is Eulerian, giving reasons.
   2. State whether it is Hamiltonian, giving reasons.
   3. Give the Hamiltonian closure.
   In each case either give the relevant cycle or explain why it does not exist.

   1. 
      

   2. 
      

   3. 
      

   4. 
      

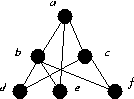
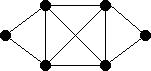
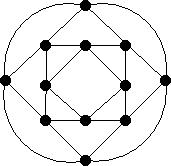
2. (Ex 6.12) Let G be a 3-regular graph of order 12 and H a 4-regular graph of order 11.
   1. Is G + H Eulerian?
   2. Is G + H Hamiltonian?

3. 1. For what values of n and m is K_n,m Eulerian?
   2. Find Conditions on n and m so that K_n,m is guaranteed to be Hamiltonian?

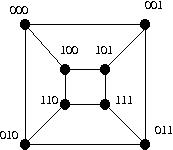
4. Consider the graph Q₃ below. For each of the matchings given below
   1. Find an M-alternating path which is not M-augmenting.
   2. Find an M-augmenting path P.
   3. Use P to produce a larger matching.

   

   1. M = empty.
   2. M = { (000, 010), (111, 011), (110, 100) }
   3. M = { (011, 001), (110, 010), (110, 100) }

5. Find the size of a maximal matching in each case: (Hint: Consider the cases n odd and n even separately.)
   1. K_n
   2. C_n
   3. P_n
   4. K_n,m

6. For this question we assume that T is a tree with a perfect matching M.
   1. Show that every leaf in T has a unique parent.
   2. Show that the graph formed by deleting all the leaves of T and their parents has a perfect matching.
   3. Use the above results to create an algorithm for finding a perfect matching on a tree or determining if one does not exist.
   4. Conclude that every tree has at most one perfect matching.

Peter Danziger, March 2008