MTH 607 Graph Theory Lab 9 - Solutions

1. State whether it is Eulerian, giving reasons.
2. State whether it is Hamiltonian, giving reasons.
3. Give the Hamiltonian closure.

1. 
   
   1. Not Eulerian since it contains odd degree vertices. For example a is an odd degree vertex.
   2. Not Hamiltonian.

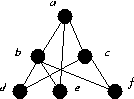
      By the Heuristic, since d and f are degree 2, we must use edges bdc and cfb. Putting these together gives the closed circuit bdcfb.

      Alternately, By the Heuristic, since d, e and f are degree 2, we must use edges bdc, bea and cfb. But now b has been used 3 times.

   3. Add edges bc and ce.

2. 
   
   1. Is Eulerian, every vertex is of even degree.
   2. Is Hamiltonian, Hamiltonian circuit is the outside cycle.
   3. The Hamiltonian closure is itself, ie. C(G) = G.

3. 
   
   1. Not Eulerian, all vertices have degree 3.
   2. Hamiltonian.
   3. C(Q₃) = Q₃.

4. 
   
   1. Eulerian, all vertices have degree 4.
   2. Not Hamiltonian (?).
   3. C(G) = G.

1. Is G + H Eulerian?
2. Is G + H Hamiltonian?

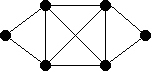
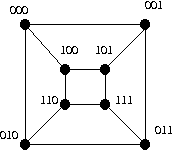
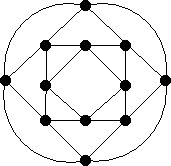
For v &isin V(G), d(v) = 3 + 11 = 14.
For v &isin V(H), d(v) = 4 + 12 = 16.

1. Is G + H Eulerian?

   So every vertex has even degree and hence is Eulerian.

2. Is G + H Hamiltonian?

   Note that there are 23 vertices in total. For any pair of vertices u and v, either:
   both are from G and so d(u) + d(v) = 14 + 14 = 28.
   both are from H and so d(u) + d(v) = 16 + 16 = 32.
   One from each and so d(u) + d(v) = 14 + 16 = 30.
   In every case d(u) + d(v) > 23 and so the graph is Hamiltonian.

1. For what values of n and m is K_n,m Eulerian?

   n and m both even.

2. Find Conditions on n and m so that K_n,m is guarenteed to be Hamiltonian?

   n = m.

For each of the matchings given below

1. Find an M-alternating path which is not M-augmenting.
2. Find an M-augmenting path P.
3. Use P to produce a larger matching.

1. M = empty.
   1. Any non empty path is M-augmenting and zny edge is M-alternating, so there is no such path.
   2. Any edge is M-alternating, I will use (000, 001).
   3. M' = (000, 001).

2. M = { (000, 010), (111, 011), (110, 100) }
   1. 100, 000, 010, 011, 111
   2. 100, 000, 010, 011, 111, 101
   3. { (100, 000), (010, 011), (111, 101), (110, 100) }.

3. M = { (011, 001), (110, 010), (110, 100) }

   This is not a matching since 110 appears twice. We can still find an M-alternqating path (eg 100, 011, 111), but not M-augmenting ones

1. K_n

   n/2 if n is even and (n-1)/2 if n is odd.

2. C_n

   n/2 if n is even and (n-1)/2 if n is odd.

3. P_n n/2 if n is even and (n-1)/2 if n is odd.

4. K_n,m

   min(n,m)

1. Show that every leaf in T has a unique parent.

   Since T is a tree it is bipartite and so Hall's Theorem applies.
   Since M is a perfect matching both parts are saturated.
   Thus for every S ⊂ V(T), |S| ≤ |N(S)|.
   In particular this implies that no two leaves have the same parent.

2. Show that the graph formed by deleting all the leaves of T and their parents has a perfect matching.

   Since M is a perfect matching it covers every vertex of T.
   In particular it must cover every leaf of T.
   Thus (l,p) ∈ M, for every leaf l and its parent P.
   Let T' be the graph obtained by deleting all the leaves of T and their parents.
   Consider M restricted to T', this is a perfect matching on T'.
   

3. Use the above theorems to create an algorithm for finding a perfect matching on a tree or determining if one does not exist.

   Input a tree T.
   

   while(1) {
   	If T = empty return success.
   	S = empty
   	For each leaf l of T {
   		Let p be l's parent.
   		If p is already in M return "No perfect matching exists"
   		Otherwise add the edge (l,p) to M.
   		S = S ∪ {l, p}
   	}
   	T = T - S
   }

Peter Danziger, March 2008