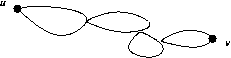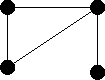
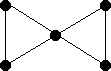
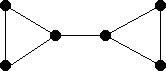
1. Find the line graphs of the graphs below.

   	Kite		Bowtie		Dumbell

2. 1. Find the line graph of the hypercube Q₃.

   2. Show that if a graph is r regular then its line graph is 2(r-1) regular.

3. 1. Show that given a cycle v₀ v₁, ..., v_k in the line graph of G, the corresponding edges in G also form a cycle.
   2. Use the result of a above to show that the line graph of a tree is a tree.

4. (Ex 5.33) Let G be a 5-connected graph, show that between any 3 distinct vertices u, v and w there are 2 cycles which have C and C' which have only the points u and v in common and do not go through w.

5. Given a graph G and a pair of points u, v ∈ V(G), a uv-necklace is a sequence of cycles C₁, C₂, . . . , C_k such that
   1. u is in C₁ and v is in C_k;
   2. C_i, C_i+1 meet in exactly 1 point;
   3. C_i, C_j have no points in common when |i - j| ≠ 0, 1.
   

   Show that a graph is 2-edge connected if and only if there is a uv-necklace for every pair of vertices u and v. (You may use Menger's Theorem).

Peter Danziger, March 2008