1. Find the line graphs of the graphs below.

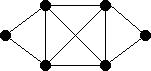
   Graph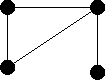
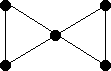
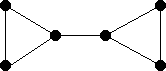
   Line Graph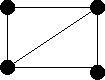
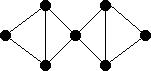
   	Kite		Bowtie		Dumbell

2. 1. Find the line graph of the hypercube Q₃.
      

   2. Show that if a simple graph is r regular then its line graph is 2(r-1) regular.

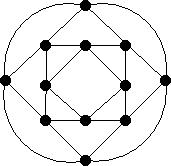
      Consider an edge e = xy of an r regular graph G.
      The edge is incident on r - 1 edges at x and r - 1 edges at y.
      This gives 2(r-1) edges incident with e in G.

3. 1. Show that given a cycle v₀ v₁, ..., v_k in the line graph of G, the corresponding edges in G also form a cycle.

      Given an edge of G (vertex of L(G)), v_i, then v_i is adjacent to v_i-1 and v_i+1 in G. (arithmetic modulo k)
      If two edges in G are incident in G, this would close the cycle in L(G).
      Thus going around the cycle in L(G) gives a cycle in G.

   2. Use the result of a above to show that the line graph of a tree is a tree.

4. (Ex 5.33) Let G be a 5-connected graph, show that between any 3 distinct vertices u, v and w there are 2 cycles which have C and C' which have only the points u and v in common and do not go through w.

   Let u, v and w be distinct vertices of a 5-connected graph, G.
   Since G is 5-connected, there are at least 5 internally disjoint uv-paths.
   At most one of these paths go through w.
   The remaining 4 paths form 2 cycles which have only the points u and v in common and do not go through w.

5. Given a graph G and a pair of points u, v ∈ V(G), a uv-necklace is a sequence of cycles C₁, C₂, . . . , C_k such that
   1. u is in C₁ and v is in C_k;
   2. C_i, C_i+1 meet in exactly 1 point;
   3. C_i, C_j have no points in common when |i - j| ≠ 0, 1.
   

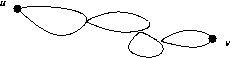
   Show that a graph is 2-edge connected if and only if there is a uv-necklace for every pair of vertices u and v.

   (⇒) Let G be a 2-edge connected graph and let u and v be any pair of vertices in V(G).
   Now by Menger's Theorem (edge version) there are at least two edge disjoint uv-paths, P and Q.
   Each time P and Q share a point they create a cycle. Sharing many points creates a necklace.

   (⇐) Let G be a graph for which every pair of vertices u and v is joined by a uv-necklace.
   This means that every pair of points is joined by 2 edge disjoint paths and so G is 2-edge connected by Mengers Theorem (edge version).

Peter Danziger, March 2008