Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 7 - Solutions

We will work on these questions in the lab.

  1. For the graphs below:
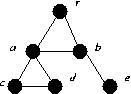
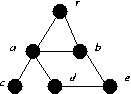
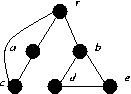
    G1 G2 G3
    1. Find all cut vertices.

      G1: a and b.

      G2: a.

      G3: r and b..

    2. Find all bridges

      G1: be

      G2: ac

      G3: rb

    3. Find the blocks of the graphs.

      G1: {r, a, b}, {a, c, d}, {b, e}.

      G2: {r, a, b, d, e}, {a, c}.

      G3: {r, a, c}, {b, d, e}, {r, b}.

    4. Trace through the block finding algorithm and indicate the P value of each vertex, its parent and block.

    1. (Book 5.12) If a graph contains 3 blocks and k cut vertices, what are the possible values of k?

      Since blocks can intersect in at most one articulation point, There are from 0 to 3 cut vertices. (Draw the pictures.)

    2. Show that if a connected graph G with k blocks B1 . . . Bk then
      n(G) = [ Σk i=1 n(Bi) ] - k + 1
      Where n(X) is the number of points in X.

      Let G be a graph with k blocks B1 . . . Bk.

      The total number of points in all the blocks is Σk i=1 n(Bi)
      We know that any pair of blocks intersects in at most 1 point, so there are at most k - 1 points which appear in two blocks and have been double counted.
      So n(G) ≥ [ Σk i=1 n(Bi) ] - k + 1.
      But since G is connected there must be a path from any point in one block to any point in another block, so there must be exactly k - 1 intersection points. Thus we have equality.

    3. Consider the statement P:
      If e is a cut edge of a graph then one of the vertices of e is a cut vertex.
    1. Give a counterexample to show that the P is false.

      K2

    2. Think of a condition to add to this statement which would make P true.

      Add "with at least three vertices."

    3. Prove the amended statement.

      Let G be a graph with at least 3 vertices and let e = uv be a cut edge of G.
      Since G is connected and has more than 3 vertices, we have that one of u or v has degree greater than 1. We suppose that d(u) > 1.
      Now since d(u) > 1, and e is a cut edge there is some w ∈ V(G) with w adjacent to v and u and w in different components of G - e.
      This means that every uw-patyh goes through v, and so G - v has u and w in different components.
      Thus v is an articulation point of G.

  4. The graph Q3 below is both 3-connected and 3-edge connected.
    1. Find three internally disjoint paths between
      1. 000 and 011;

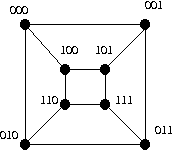
        d P1 = 000, 001, 011
        P2 = 000, 010, 011
        P3 = 000, 100, 110, 111, 011

      2. 000 and 101.

        P1 = 000, 001, 101
        P2 = 000, 010, 110, 100, 101
        P3 = 000, 100, 101

    2. Find three edge disjoint disjoint paths between.
      1. 000 and 011;
      2. 000 and 101.

      Same as part a.

  5. Show that if a graph G has the property that for every edge e there are three cycles C1, C2 and C3 in G whose only common edge is e then G is 3-edge connected.

    Use this to show that the Peterson graph is 3-connected.

  6. Given a graph G and a pair of points u, v ∈ V(G), a uv-necklace is a sequence of cycles C1, C2, . . . , Ck such that
    1. u is in C1 and v is in Ck;
    2. Ci, Ci+1 meet in exactly 1 point;
    3. Ci, Cj have no points in common when |i - j| ≠ 0, 1.

    Show that a graph is 2-edge connected if and only if there is a uv-necklace for every pair of vertices u and v.

    (⇒) Let G be a 2-edge connected graph and let u and v be any pair of vertices in V(G).
    Now by Menger's Theorem (edge version) there are at least two edge disjoint uv-paths, P and Q.
    Each time P and Q share a point they create a cycle. Sharing many points creates a necklace.

    (⇐) Let G be a graph for which every pair of vertices u and v is joined by a uv-necklace.
    This means that every pair of points is joined by 2 edge disjoint paths and so G is 2-edge connected by Mengers Theorem (edge version). -->