Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 6

We will work on these questions in the lab. These questions will refer to the following graphs:
G1 G2 Q3

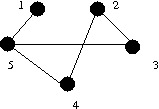
    1. For G1 find [ {2, 4}, {1, 3, 5} ].
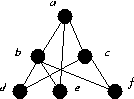
    2. For G2 find [ {b, c, e}, {a, d, f} ].
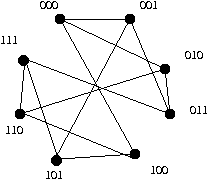
    3. For Q3 find [ {000, 011}, comp({000, 011}) ], where comp(S) is the complement of S.

  2. For each of the graphs above find the following:
    1. A vertex cut set of size 2, or explain why no such exists.
    2. An edge cut set of size 2, or explain why no such exists.
    3. The vertex connectivity K(G).
    4. The edge connectivity K'(G).

  3. Find the vertex and edge connectivity of the Peterson Graph.

  4. Find graphs G which satisfy each of the following:
    1. K(G) = K'(G) = δ(G)
    2. K(G) = K'(G) < δ(G)
    3. K(G) < K'(G) = δ(G)
    4. K(G) < K'(G) < δ(G)

  5. Let T be a tree:
    1. Use the fact that there is a unique path between any pair of vertices in a tree to show that if v is an internal vertex of T then T - v is not connected.
    2. If v is a leaf in a tree T show that T - v is connected.

  6. Let G be a connected graph with at least three vertices. Form G' from G by adding an edge between every pair of vertices which are distance 2 apart in G. Show that G' formed in this way is 2-connected.