MTH 607 Graph Theory Lab 6 Solutions

1. For G₁ find [ {2, 4}, {1, 3, 5} ].

   { 23, 45 }

2. For G₂ find [ {b, c, e}, {a, d, f} ].

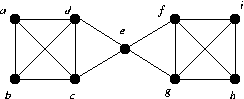
   ab, ac, ae, bd, bf, cd, cf

3. For Q₃ find [ {000, 011}, comp({000, 011}) ], where comp(S) is the complement of S.

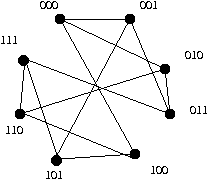
   000 001, 000 010, 000 100, 011 010, 011 001, 011 111.

1. A vertex cut set of size 2, or explain why no such exists.

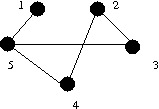
   G₁: { 2, 5 }

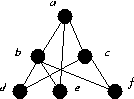
   G₂: { b, c }

   Q₃: There is no cut set of size 2 as the graph is 3-connected.

2. An edge cut set of size 2, or explain why no such exists.

   G₁: { 35, 45 }

   G₂: { bd, cd }

   Q₃: There is no edge cut set of size 2 as the graph is 3-edge connected.

3. The vertex connectivity K(G).

   K(G₁) = 1 as 5 is an articulation point.

   K(G₂) = 2 { b, c } is a cut set, but every point lies on a cycle.

   K(Q₃) = 3 As noted there is no 2 cut set, but { 000, 011, 101 } is a cut set.

4. The edge connectivity K'(G).

   K'(G₁) = 1, as 15 is a cut edge.

   K'(G₂) = 2, { db, dc } is a cut set, but every point lies on a cycle.

   K'(Q₃) = 3, As noted there is no 2 edge cut set, but { 000 001, 000 010, 000 100 } is a cut set.

3 in each case.
Note that since the Peterson graph is 3-regular we know that the vertex and edge connectivity are the same.
Since the minimum degree δ = 3, we know that they are at most three.
Use the symmetry of the graph to argue that no 2-edge cut can disconnect the graph.

1. K(G) = K'(G) = δ(G)

   K_n, K_m,n, P_n, C_n, peterson.

2. K(G) = K'(G) < δ(G)

   

3. K(G) < K'(G) = δ(G)

   

4. K(G) < K'(G) < δ(G)

   

1. Use the fact that there is a unique path between any pair of vertices in a tree to show that if v is an internal vertex of T then T - v is not connected.

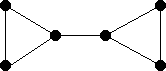
   By the definition of internal d(v) > 1, so v has at least two neighbors in T, u₁ and u₂ say.
   But since T is a tree there is a unique path from u₁ to u₂, which must be { u₁, v, u₂ }
   Now T - v has no u₁ u₂--path, and so is disconnected.

2. Show that if v is a leaf in T then T - v is connected.

   Let T be a tree and v a leaf of T.
   By the definition of leaf d(v) = 1, so v has exactly one neighbor, u say.
   Let x and y be any pair of vertices in T - v.
   Since T is a tree there is a unique xy--path in T, P say.
   The degree of an internal vertex of a path must be at least 2, but the degree of v is one, so v does not appear as an internal vertex of P.
   Thus P only contains vertices in T - v and so connects x and y in T - v.

Let G be a connected graph with at least three vertices.
Let G' be formed from G by adding an edge between every pair of vertices which are distance 2 apart in G.
Clearly any cut vertex of G' is also a cut vertex of G since we have only added edges.
Suppose u is a cut vertex of G and let x and y be in different components of G - u.
Since G is connected there must be an paths from x to u and v to w where v and w are neighbors of u.
But since v and w are both neighbors of u they are distance 2 apart in G and so have an edge between them in G'.
Thus there is an xy-path in G - u.