MTH 607 Graph Theory Lab 5

1. Identify the leaves of T.

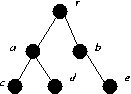
   c, d, e

2. Identify the internal vertices of T.

   r, a, b

3. What is the height of T?

   2

4. Is T a binary tree?

   Yes. Each vertex has at most two children.

5. List the vertices of the left subtree of r.

   a, c, d

6. Find a bipartition of T.

   { r, c, d, e }, { a, b }.

Yes. There are two perfectly good explanations:

1. By definition a tree contains no cycles. In particular it contains no odd cycles. But a graph with no odd cycles is bipartite.

2. Pick a vertex of the tree, and put it in one part, put all its neighbours in th other part and all their neighbors in the first part and so on. This process must terminate since the tree is finite and we will never get a conflict since this would imply a cycle.

The first is simpler, but the second actually provides you with the bipartition.

1. Find all trees on 4 vertices, up to isomorphism.

2. Find all binary trees on 4 vertices, up to isomorphism.

1. Find a spanning tree of G.

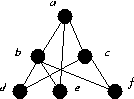
   The tree in question 1.

2. Identify the fundamental circuits of G with respect to your spanning tree.

   Given the spanning tree above the fundamental circuits are: C(dc) = abdca, C(ea) = abea, C(bf) = abfca.

3. Use your answer to give the number of circuits in G.

   There are three fundamental circuits above, these can be combined in 4 ways (C(dc) ⊕ C(ea), C(dc) ⊕ C(bf), C(bf) ⊕ C(ea), C(dc) ⊕ C(bf) ⊕ C(ea) to give three more, for a total of 7.

4. Consider the following graphs.

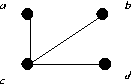
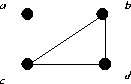
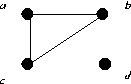
   G1		G2		G3

   1. Find G₁ ⊕ G₂.
      
   2. Find G₃ ⊕ G₂.
      
   3. Is G₁ ⊕ G₂ ≅ G₁ ⊕ G₃?

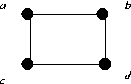
      G₁ ⊕ G₂ is given in part a, G₁ ⊕ G₃ =

      

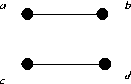
      Take the mapping from G₁ ⊕ G₂ to G₁ ⊕ G₃ given by
      a -> a, b -> c, c -> b, d -> d;
      or
      a -> d, b -> b, c -> c, d -> a.

5. Is it true that the ring sum of two trees is a tree?

   No. It is easy to come up with a counterexample.