Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 4 Solutions

  1. For each of the following find the order of the given function.
    1. f(x) = x2 + 2x

      O(2x) - Exponential

    2. f(x) = 17 + 24 × 5

      O(c) - Constant

    3. f(n) = 37n! + 2n

      O(n!) - Factorial

    4. f(x) = 4,982,734 + 49,827,420x + 3458291x2 + ½x3

      O(x3) - Cubic

    5. f(n) = (1 + n) log n

      O(n) - Loglinear

    6. f(n) = log [n(1 + n)]

      O(logn) - Logarithmic

  2. Show that for any positive functions f, g and h, if f(x) ∈ O(h(x)) and g(x) ∈ O(h(x)) then the function (af(x) + bg(x)) ∈ O(h(x)) for every real number a and b. (Hint: Use the limit definition of O, quote any properties of limits you use.)

    We will use the following two theorems on limits.

    Theorem 1 If a ∈ R and limx = L → ∞ f(x) < ∞ then limx → ∞ af(x) = aL.

    Theorem 2 If limx = L → ∞ f(x) < ∞ and limx → ∞ g(x) = M < ∞ then limx → ∞ f(x) + g(x) = L + M.

    Suppose that f(x) ∈ O(h(x)) and g(x) ∈ O(h(x)).
    Thus limx → ∞ f(x)/ h(x) = L < ∞ and limx → ∞ g(x)/ h(x) = M < ∞.

    Now for any a, b ∈ R limx → ∞ af(x)/ h(x) = aL < ∞ and limx → ∞ bg(x)/ h(x) = bM by Theorem 1.

    So limx → ∞ af(x)/ h(x) + bg(x)/ h(x) = aL + bM < ∞, by Theorem 2.
    So f(x) + g(x) ∈ O(h).

  3. For this question let A =
    v1 v2 v3 v4 v5
    0 0 0 0 1
    0 0 1 1 0
    0 1 0 0 1
    0 1 0 0 1
    1 0 1 1 0

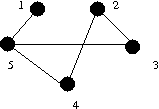
    1. Given the adjacency matrix A above, draw the corresponding graph G.

    2. Write down the corresponding adjcency list for G.

      Index Pointer Vertex
      1: 0 5
      2: 6 3
      3: 7 2
      4: 8 2
      5: 9 1
      6: 0 4
      7: 0 5
      8: 0 5
      9: 10 3
      10: 0 4

    3. Write down the corresponding adjcency table for G.

      1: 5
      2: 3, 4
      3: 2, 5
      4: 2, 5
      5: 1, 3, 4

    4. Use the adjacency matrix method to find the number of paths of length 3 from v1 to v2. Identify these paths on your picture.
      A2 =
      1 0 1 1 0
      0 2 0 0 2
      1 0 2 2 0
      1 0 2 2 0
      0 2 0 0 3
      		A3 =
      0 2 0 0 3
      2 0 4 4 0
      0 4 0 0 5
      0 4 0 0 5
      3 0 5 5 0
      Hence there are 2 paths from v1 to v2.

    5. Since there is no edge between v1 and v2 W0(v1, v2) = ∞. Without calculating them explain why W1(v1, v2) = W2(v1, v2) = ∞

      Wk(vi, vj) represents the length of the shortest path from vi to vj using only vertices from v1 to vk internally, or ∞ if no such path exists.

      Thus W1(v1, v2) is the length of the shortest path from v1 to v2 using only v1 internally. But there is no edge v1 v2, so this is ∞.

      A similar argument holds for W2(v1, v2).

    6. Find Wk(v1, v2) for k = 3, 4 and 5.

      First note that Wk(v1, vk) = ∞ for every k < 5, since every path to v1 must pass through the point v5. This argument saves a lot of calculation. Further note that Wk(vi, vj) = 1 if and only if there is an edge between vi, vj.

      Now W5(v1, v2) = min(W4(v1, v2), W4(v1, v5) + W4(v5, v2)).
      Firstly, W4(v1, v5) = 1 since there is an edge between them.
      Further W4(v5, v2) = min(W3(v5, v2), W3(v5, v4) + W3(v4, v2) ).
      W3(v4, v2) = W3(v5, v4) = 1, since there is an edge between them.
      So W4(v5, v2) = 2.

      Thus W5(v1, v2) = 3.

      The point of this question was to show that calculations of the W's can be long, though I have used quite a few shortcuts here.

    7. Draw the shortest path(s) from v1 to v2, how many are there?

      Not shown.

    1. Given a graph with 1,000 vertices, if we use the "W" method to find the length of shortest path between to given points, roughly how many steps would you expect to use?

      To find Wk(vi, vj) we must find Wk-1(vi, vj) for each pair i, j ≤ k, giving k choose 2 = k(k-1)/2. This yields k(k-1)/2 calculations at each level. We must find Wn(vi, vj) for each i and j, giving

      &Sigmak=1n (k(k-1)/2) = ½ &Sigmak=1n (k2 - k) = (n(n+1)(2n+1)/6 - n(n+1)/2) ∈ O(n3)
      Where I have used the formulas &Sigmak=1n (k) = n(n+1)/2 and &Sigmak=1n (k2) = n(n+1)(2n+1)/6.

    2. Can you think of an algorithm based on matrix multiplication to find the shortest path between two given points?

      If the vi, vj entry of Ak is non zero it means there is a path of length k. This suggests the following algorithm:

      Find succesive powers of the adjacency matrix until the vi, vj entry is non zero.

    3. Given that matrix multiplication is roughly O(n2) what is the complexity of your algorithm?

      In the worst case we must calculate n matrix products, each taking O(n2) steps, for a total of roughly O(n3).

      Note that this is the same as the W method.

  5. For each of the graphs below
    1. Find a DFS ordering of the vertices.
    2. Find a BFS ordering of the vertices.
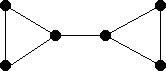
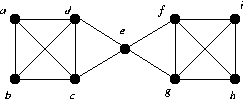
    Graphs: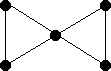
    NameBowtie Dumbell Extended Bowtie
    Start Central vertex One of the central vertices e

Maintained by: P. Danziger, February 2007.