Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 3

  1. (Book 2.32 a,c,d) For each of the following sequences determine wether they are graphical. If they are draw a graph with the given sequence as its degree sequence. If not explain why not.
    1. 5, 3, 3, 3, 3, 2, 2, 2, 1.
    2. 6, 5, 5, 4, 3, 2, 1.
    3. 7, 5, 4, 4, 4, 3, 2, 1.

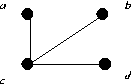
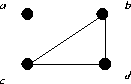
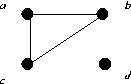
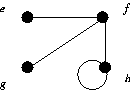
  2. Consider the following graphs.
    G1 G2 G3
    1. Find G1 ∪ G2, the Union of G1 with G2 (Be very careful when answering this question)
    2. Find G2 ∪ G3, the Union of G2 with G3 (Be very careful when answering this question)
    3. Find G1 + G2, the join of G1 with G2.
    4. Find G1 × G2, the cartesian product of G1 with G2.
    5. Find G1 ⊗ G2, the extended cartesian product of G1 with G2.

  3. Show that the graphs below are isomorphic.
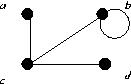
    G1 G2

  4. Give three graphs which have the same number of vertices and the same degree sequence, but are not isomorphic.

  5. Book 3.8.

  6. (Book 3.16) How many nonisomorphic simple graphs have degree sequence 6, 6, 6, 6, 6, 6, 6, 6, 6?
    (Hint Consider the complement of G.)

  7. Show that K2 × K2 × K2 ≅ C4 × K2 ≅ Q3.

  8. List all simple graphs on 4 vertices, up to isomorphism.

Maintained by: P. Danziger, January 2007.