MTH 607 Graph Theory Lab 3

1. 5, 3, 3, 3, 3, 2, 2, 2, 1.

   Applying the Sequence Theorem (2.10), this sequence is graphical if and only if
   s₁: 2, 2, 2, 2, 2, 2, 1, 1 is graphical.
   s₁ is the degree sequence of the path P₈. So the final answer is P₈ with an extra vertex joined to five of the internal degree 2 vertices of the path.

2. 6, 5, 5, 4, 3, 2, 1.

   Applying the Sequence Theorem (2.10), this sequence is graphical if and only if
   s₁: 4, 4, 3, 2, 1, 0 is graphical.
   Again applying the Sequence Theorem (2.10) again, we get that s₁ is graphical if and only if
   s₂: 3, 2, 1, 0, 0 is.
   Continuing, we get that s₂ is graphical if and only if
   s₃: 1, 0, -1, 0 is.
   Clearly this is not graphical as it contains a negative integer. Recursing back up the chain we have that the original sequence is not graphical.

3. 7, 5, 4, 4, 4, 3, 2, 1. Successively applying the Sequence Theorem (2.10), this sequence is graphical if and only if thew following are graphical
   s₁: 4, 3, 3, 3, 2, 1, 0.
   s₂: 2, 2, 2, 1, 1, 0.
   s₂ is the degree sequence of a path P₅ together with an isolated point, so the original sequence is graphical.

   To draw the graph start with P₅ ∪ { v }.
   Add a new point v₂ joined to each of the internal vertices of the P₅ and one of the endpoints. This graph G₁ has degree sequence s₁.
   Now add a new point v₁ and adjoin it to every point in G₁ to get a graph with the original degree sequence.
   So G = G₁ + { v₁ }.

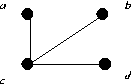
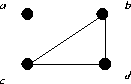
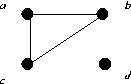
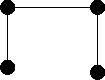
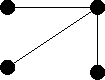
G1		G2		G3

1. Find G₁ ∪ G₂, the Union of G₁ with G₂ (Be very careful when answering this question)
2. Find G₂ ∪ G₃, the Union of G₂ with G₃ (Be very careful when answering this question)
3. Find G₁ + G₂, the join of G₁ with G₂.
4. Find G₁ × G₂, the cartesian product of G₁ with G₂.
5. Find G₁ ⊗ G₂, the extended cartesian product of G₁ with G₂.

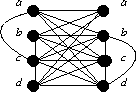
   Not Shown

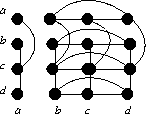
G1		G2

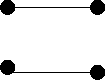
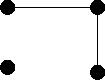
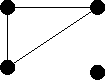
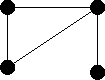
The isomorphism is given by the following mapping f from G₁ to G₂:

Note that there are many possible solutions to this question. Here is a non simple one.

All have degree sequence 2,3,3.

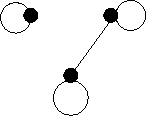
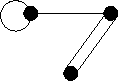
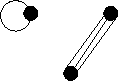
For a simple solution take the graphs: C₈, C₅ ∪ C₃ and C₄ ∪ C₄. All have 8 points and are 2-regular, and so degree sequence 2, 2, 2, 2, 2, 2, 2, 2.

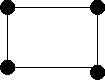
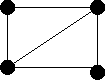
G₁ is isomorphic to G₂, they are both isomorphic to Q₃. They are not isomorphic to G₃, probably the easiest way to see this is to note that G₃ is not bipartite, whereas the other two are.

This is a 6 regular graph on 9 points, so its complement will be 2-regular on 9 points, and so is a collection of cycles. Up to isomorphism there are only 4 possible collections of cycles on 9 points: C₉, C₆ ∪ C₃, C₅ ∪, C₄ and C₃ ∪ C₃ ∪ C₃.

Thus up to isomorphism there are 4 possible 6-regular graphs on 9 points, given by the complements of the graphs above.

See book, p. 25.
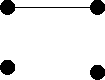