Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 2

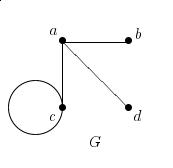
  1. For the graph G given above give the following, or explain why the graph does not have the given property. (Quote any theorems you use.)
    1. d(c).
    2. The degree sequence.
    3. The adjacency matrix.
    4. A bipartition.
    5. An articulation point.
    6. The blocks of G.
    7. The subgraph of G induced by S = { a, c }.

  2. For each of the following either explain why the specified graph cannot exist (quote any theorems you use), or draw a graph with the given property.
    1. A graph with degree sequence 3, 1, 1.
    2. A graph with degree sequence 4, 3, 3.
    3. A simple graph with degree sequence 4, 3, 3.
    4. A 3 regular graph on 9 vertices.
    5. A simple graph with 3 connected components on 5 vertices.

  3. Find two non-isomrphic 3-regular graphs.

  4. Give three graphs which have the same order and the same degree sequence, but are not isomorphic.

  5. Show that in a disconnected graph there must be a path from any vertex of odd degree to some other vertex of odd degree.

  6. Suppose v is a vertex of a connected simple graph G. Prove that v has a neighbor in every component of G-v.

Maintained by: P. Danziger, January 2007.