Ryerson Crest Ryerson Header

MTH 607 Graph Theory Lab 2 Solutions

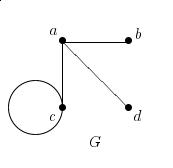
  1. For the graph G given above give the following, or explain why the graph does not have the given property. (Quote any theorems you use.)
    1. d(c).
      3
    2. The degree sequence.
      3, 3, 1, 1.
    3. The adjacency matrix.
      a:0 1 1 1
      b:1 0 0 0
      c:1 0 2 0
      d:1 0 0 0
    4. A bipartition.
      There is no bipartition. The graph contains a loop, and no graph containing a loop is bipartite.
    5. An articulation point.
      a
    6. The blocks of G.
      The graphs induced by: {a, b}, {a, d}, {a, c} are the blocks of G.
    7. The subgraph of G induced by S = { a, c }.
      Don't forget the loop!

  2. For each of the following either explain why the specified graph cannot exist (quote any theorems you use), or draw a graph with the given property.
    1. A graph with degree sequence 3, 1, 1.
      Impossible - odd number of vertices with odd degree.
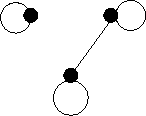
    2. A graph with degree sequence 4, 3, 3.
      One of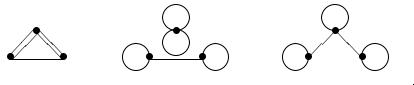
      or A triangle (K3) with a loop on one vertex and a double edge on the opposite edge.
    3. A simple graph with degree sequence 4, 3, 3.
      DNE. TD = 4 + 3 + 3 = 10 > 3(2) = 6.
    4. A 3 regular graph on 9 vertices. DNE. Both are odd.
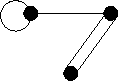
    5. A simple graph with 3 connected components on 5 vertices.
      One of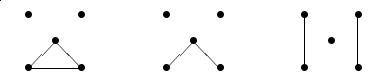

  3. Find two non-isomrphic 3-regular graphs.
    H10,3 and the Peterson graph.

  4. Give three graphs which have the same order and the same degree sequence, but are not isomorphic.

    Note that there are many possible solutions to this question.

    All have degree sequence 2,3,3.

    Another solution with simple 2-regular graphs is to take the three graphs 3C3, C4 ∪ C5, C9

  5. Show that in a disconnected graph there must be a path from any vertex of odd degree to some other vertex of odd degree.

    Proof: Given a disconnected graph G, let v be a vertex of odd degree.
    Let H be the connected component of G containing v.
    Considering H as a graph in its own right, H must have another vertex w of odd degree, (number of odd degree vertices is even).
    Since H is connected there is a path from v to w.

  6. Suppose v is a vertex of a connected simple graph G. Prove that v has a neighbor in every component of G-v.

    Proof: Let G be a graph and let v be a vertex of G.
    Let H be a connected component of G - v and let u be any vertex of H.
    Since H is connected, there is a vu-path, the first vertex on this path is a neighbour of v in H.

Maintained by: P. Danziger, January 2007.