1. Find a 2-factorization of the following, or explain why no 2-factorization exists:
   1. K_4,4
   2. K₈
   3. K₉

2. 1. Find a decomposition of the bowtie into triples (C₃)

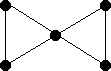
   2. Find a decomposition of the graph below into cycles. Explain why no C₃ decomposition can exist.
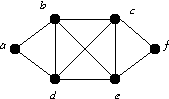
   3. Find a decomposition of Q₃ into a 1-factor and a 2-factor.

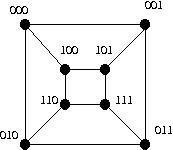
   4. Find a factorization of the K₁₅ into triples (C₃)

      This is the original Kirkman's Schoolgirl Problem:

      Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily so that no two shall walk twice abreast.

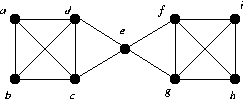
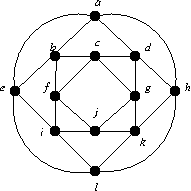
3. Find the chromatic number χ(G) and the chromatic index χ'(G) for each of the graphs below. In each case give the colour classes of a minimal colouring.

   (a)		(b)		(c)
   (d)		(e)

4. Given a minimum colouring of a graph G, show that for each colour class C_i there is some vertex v ∈ C_i which is adjacent to a vertex of each of the other colours.

5. Let G be a k-regular bipartite graph, show that G has an r-factorization if and only if r divides k.
   (You may assume that every k-regular bipartite graph has a 1-factorization.)

Peter Danziger, April 2008