1. For each of the following graphs find a 1-factor or explain why one cannot exist (via Tuttes). ie Find a set S such that |S| < |o(G-S)|.
   1. 

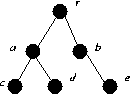
      G - a has three odd components.

   2. 

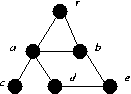
      Take S = ∅ in Tutte's.

   3. 

      ca, rb, de is a 1-factor.

   4. 

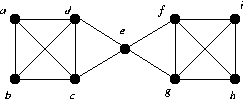
      The to end edges, together with the bar of the dumbell form a 1-factor.

   5. 

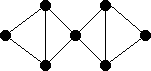
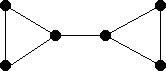
      Removing the central vertex gives two odd components, so |S| = 1 but o(G - S) = 2. So no 1-factor exists.

   6. 

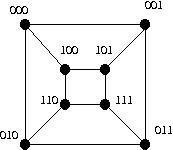
      { (000, 001), (010, 011), (100, 101), (110, 111) }

2. Use Tuttes Theorem to show that K_3,5 does not have a 1-factor.

   Removing the part of size three leaves five components of odd size. So |S| = 3 and o(G - S) = 5.

3. Find a 1-factorization of the graphs below

   1. 

      { (000, 001), (010, 011), (100, 101), (110, 111) }
      { (000, 010), (001, 011), (100, 110), (101, 111) }
      { (000, 100), (001, 101), (010, 110), (011, 111) }
      

   2. 

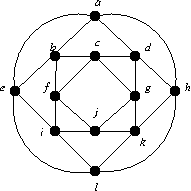
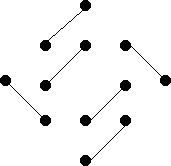
      F₁ = { (a, d), (h, k), (i, l), (b, e), (c, g), (f, j) }
      F₂ = { (a, b), (h, d), (e, i), (l, k), (c, f), (g, j) }
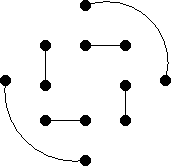
      F₃ = { (a, e), (h, l), (b, c), (d, g), (k, j), (i, f) }
      F₄ = { (a, h), (e, l), (b, f), (c, d), (g, k), (i, j) }
      

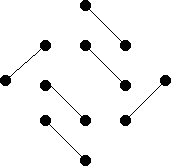
      F1		F2
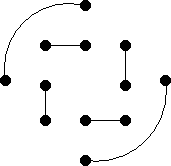
      F3		F4

4. Show that K_n,n has a 1-factorization for any n.

   Note that K_n,n is an n regular bipartite graph and hence has a perfect matching (by the Corollary to Hall's Theorem).
   Removing this perfect matching yields an (n-1)-regular bipartite graph.
   We may proceed in this manner until all edges are used.

5. Show that no tree with at least three vertices has a 1-factorization.

   Let T be a tree. Since T is a tree it has a vertex of degree 1.
   Since T is of order at least 3 it must have at least one vertex of degree greater than 1.
   Thus T is not k-regular for any k.

Peter Danziger, April 2008