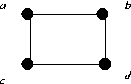
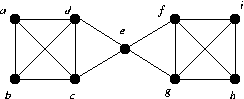
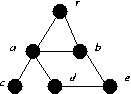
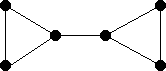
1. For each of the graphs below:
   1. Find a maximum matching.
   2. If possible find a matching which is maximal but not not maximum.
   3. If G is bipartite, with parts X, Y,
      1. List X and Y.
      2. Either find an X saturating matching (A matching which uses every point of X) or find a subset S of the vertices of G such that |S| > |N(S)|, where N(S) is the set of neighbours of points in S.
      3. Do the same for Y.

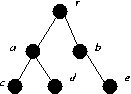
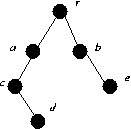
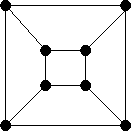
2. For each of the following graphs find
   1. α(G)
   2. α'(G)
   3. β(G)
   4. β'(G)
   5. Either find a 1-factor or explain why one cannot exist (via Tuttes Theorem).

   (a)		(b)		(c)
   (d)		(e)

3. In each case give the general class of simple connected graphs G that satisfy the given property:
   1. α(G) = 1
   2. α'(G) = 1
   3. β(G) = 1
   4. β'(G) = 1

4. 1. Show that for any graph G β(G) ≤ 2 α'(G).
   2. Find graphs for each k so that α'(G) = k and β(G) = 2k.

Peter Danziger, March 2008