MTH 607 Graph Theory Lab 10 - Solutions
-
For each of the graphs below:
- Find a maximum matching.
- If possible find a matching which is maximal but not not maximum.
- If G is bipartite, with parts X, Y,
- List X and Y.
- Either find an X saturating matching or find a set S such that |S| > |N(S)|.
- Do the same for Y.
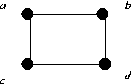
- (a, c), (b, d) or (a, b), (c, d).
- All maximal matchings are maximum.
-
- X = {a, d}, Y = {b, c}
- Either of the matchings above
- Either of the matchings above
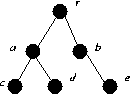
- (r, a) (b, e)
- All maximal matchings are maximum.
-
- X = {a, b}, Y = {r, c, d, e}
- (r, a), (b, e) is X saturating
- |{c, d}| = 2, but |N({c, d})| = |{a}| = 1.
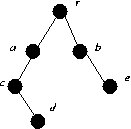
- (b, e), (a, r), (c, d)
- (b, r), (a, c)
-
- X = {r, c, e}, Y = {a, b, d}
- The answer to part a. is X saturating
- The answer to part a. is Y saturating
-
For each of the following graphs find
-
α(G)
-
α'(G)
-
β(G)
-
β'(G)
-
Either find a 1-factor or explain why one cannot exist (via Tuttes).
-

-
α(G) = 4, {r, c, d, e} is an independent set.
-
α'(G) = 2.
-
β(G) = 2 {a, b} is a vertex cover.
-
β'(G) = 4 {ac, ad, be, ra} is an edge cover.
-
Either find a 1-factor or explain why one cannot exist (via Tuttes).
G - a has three odd components so |{a}| = 1 < o(G-a)=3
and thus no one factor can exist.
-
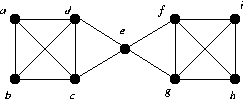
-
α(G) = 3.
-
α'(G) = 4
-
β(G) = 6.
-
β'(G) = 5.
-
Either find a 1-factor or explain why one cannot exist (via Tuttes).
G has an odd number of vertices and so cannot have a 1-factor.
Via Tuttes, S = Φ, 0 = |S| < o(G - S) = 1.
-
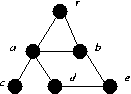
-
α(G) = 3, {r, c, e} is an independent set.
-
α'(G) = 2.
-
β(G) = 3, {a, b, d} is a vertex cover.
-
β'(G) = 4 {ac, ad, be, ra} is an edge cover.
-
ca, rb, de is a 1-factor.
-
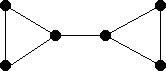
- α(G) = 2
- α'(G) = 3.
- β(G) = 3.
- β'(G) = 3.
-
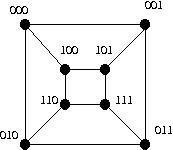
-
α(G) = 3, {000, 110, 011} is an independent set.
-
α'(G) = 4, { {000, 100}, {001, 101}, {111, 011}, {110, 010} } is a
perfect matching.
-
β(G) = 4, { 000, 110, 101, 011 } is a vertex cover.
-
β'(G) = 4. The perfect matching in ii is also a vertex cover.
- The perfect matching in ii is also a 1-factor.
-
In each case give the general class of simple connected graphs G that satisfy
the given property:
-
α(G) = 1
Kn
-
α'(G) = 1
K1,n - an n star.
-
β(G) = 1
K1,n - an n star.
-
β'(G) = 1
K2.
-
-
Show that for any graph G β(G) ≤ 2 α'(G).
Let G be a graph and let B be a minimum vertex cover.
So |B| = β(G).
Since B is incident on every edge any matching must have
each edge incident on some vertex of B.
-
Find graphs for each k so that α'(G) = k and β(G) = 2k.
A collection of triangles.
Peter Danziger, March 2008














